Fluid Filled Flexible Packaging
Clinton A. Haynes, Diana Brown, Douglas L. Marriott
Stress Engineering Services, Cincinnati, Ohio
Abstract
Drop loading is probably the most challenging load case for fluid-filled flexible packaging. Typically, manufacturers of flexible packages do not have a quantitative material test that captures both the effects of reduced ductility caused by the multi-axial stress state of the fluid-filled drop load and the high strain rate developed by the drop event. This paper discusses a cost-effective test method that has been developed to characterize the limiting ductility of flexible films in near-biaxial stress at high strain rates. The test is particularly helpful in characterizing and screening the structural performance of films and thin rigid plastics. A practical and cost-effective approach to measuring the ductility-at-fracture of films and other relatively thin materials under near-biaxial tension, as a function of strain rate, has been developed
Introduction
Most “real-world” forces and the resulting stresses that act on both rigid plastic packaging and mono- and multi-layer films are multi-axial. The sources of these forces are ubiquitous in the world of product performance; pressurization from elevation change, drop loading, assembly, and tension in a web, to name a few. Unfortunately, package and product designers typically only have uni-axial stress vs. strain data available to them because of the difficulty and cost of generating biaxial data. Since ductility can be very much reduced in bi-axial tension, compared with uni-axial tension, the consequence of this situation is that the limiting ductility of the material used in the design of products and packages in use is non-conservative. Product designers, therefore, do not have the data they need to develop product and package designs that will survive the most critical load cases.
The need for material data that is more representative of the life-limiting load cases has been and remains a growing problem. Manufacturers’ increased focus on both reduced material usage and improved sustainability demand greater performance with less material. Also, as computational methods such as non-linear finite element analysis work its way into the mainstream of the product and package development process, the need for multi-axial data is necessary to predict failure [1]. Package, product, and process designers cannot meet these challenges without having the data they need with regard to the performance of the materials they are using.
Conventional Bi-axial Testing
Although it is difficult to ever refer to bi-axial tensile testing as ‘conventional’, researchers have devised a methodology for generating near equi-biaxial tension in a specimen [4]. The fixture shown in Figure 1 illustrates a device used for low strain rate bi-axial testing. The test fixture employs a series of clamps and pulleys to apply a radially oriented displacement to the test specimen. The specimen has been designed such that the gaps between the radial “legs” do not result in a non-uniform bi-axial stress field toward the center of the test specimen.

Figure 1. Axel products mechanical biaxial/compression test fixture.
For higher strain rate bi-axial data, using a mechanical system such as that shown in Figure 1 is not practical.
Of the several methods of attaining bi-axial data at high strain rates that have been proposed, only one stands out as practical. Christensen and Feng analyzed the inflation of a thin, flat circular disk of elastomeric material and compared the results to the expected behavior based on accepted existing analytical models for plastics [3]. The analytical method developed involved inflating a thin flat plastic coupon that is clamped around its edges. The specimen is inflated, and the height of the spherical surface that develops is used to calculate the bi-axial strain at the apex of the “bubble”. Good agreement was found in this work between computational and simplified analytical prediction (Figure 2).
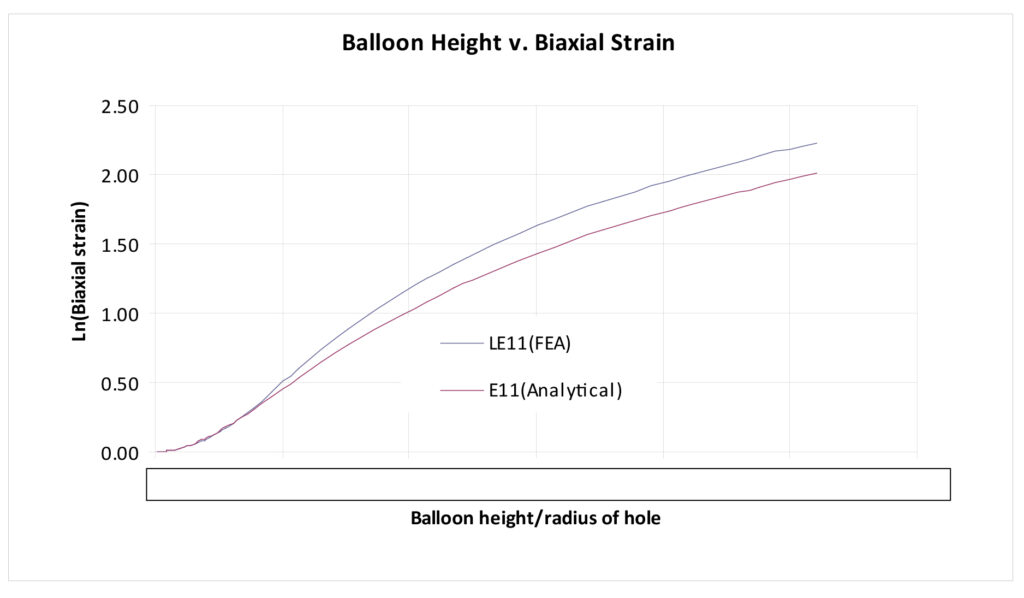
Figure 2. Comparison of Analytical and computational models
Stress Engineering Services has developed a test fixture based upon the principles discussed by Christensen and Feng to measure bi-axial material properties for films and relatively thin rigid plastics at high strain rates, such as those experienced during drop impact.
Practical Bi-axial Test Fixture
The high strain rate bi-axial inflation test fixture developed by Stress Engineering Services is shown in Figure 3. A fast response laser position sensor (1) is used to measure the height of the clamped specimen (3). Several clamps of varying opening sizes and shapes can be used to obtain varying strain rates and multi-axial stress states. A clear protective barrier (2) is used to protect the laser from the high-pressure air stream released after the test specimen bursts (4).

Figure 3. Photograph of bi-axial test fixture

Figure 4. shows the formation of the “bubble” that develops in the test specimen prior to the rupture
High-pressure plumbing components and a fast-acting solenoid connect the high-pressure gas source to the test fixture. Pressure sensors are located under the specimen and in the upstream piping. A solenoid is connected to a trigger signal through a timed relay circuit. When the solenoid is activated, high pressure gas quickly inflates the specimen to failure within a few milliseconds. The upstream pressure sensor triggers the data acquisition system which records signals from the laser and pressure sensors at high sampling rates.
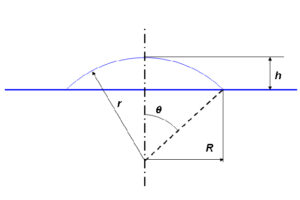
Theory
The simplified analysis used in [3] is based on the assumption that the initially flat-clamped specimen inflates in a spherical manner. The strain calculations are then derived using simple geometric relationships:
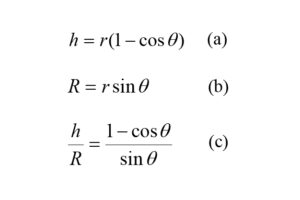
Since h and R are known quantities, θ can be solved using equation (c). With θ known, the calculation for strain is based on the fact that any 2-dimensional slice through the bubble is the change in length divided by the original length which gives the following equation for strain at the apex of the spherical section (ε) [3]:
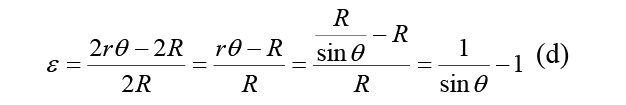
The stress in the test specimen is obtained using the following equation.
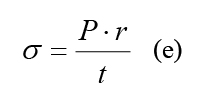
For orthotropic materials, such as polyesters, the inflation may not be spherical, which will introduce error in the calculated failure strain. The magnitude of the error is a function of the difference in strength in the orthogonal directions. However, based on practical experience to-date, the error has been relatively small. Stress Engineering Services is currently studying this behavior.
Data Analysis and Results
True stress vs. true strain is calculated from the test data. Figure 5 provides a comparison between the modulus and ductility at fracture of the multi-layer film used on a beverage pouch (Figure 6). The curves in blue are based on a uni-axial tensile test conducted at 2 inches per minute. This is the data a package designer typically has available to them when considering the structural performance of a package or product. Note the ductility at fracture is about 30% strain.
The red and pink curves are based on a bi-axial test conducted at a high strain rate. The bi-axial data is more representative of the performance-limiting material response of the pouch material with a ductility of only about 14% before fracture. Although instability occurs even in uni-axial tension at about 30%, the material continues to draw, absorbing considerable energy in a way that is not available in bi-axial tension. If the package structure was being designed to survive a drop load, the performance is limited by the bi-axial stress, not the uni-axial stress.
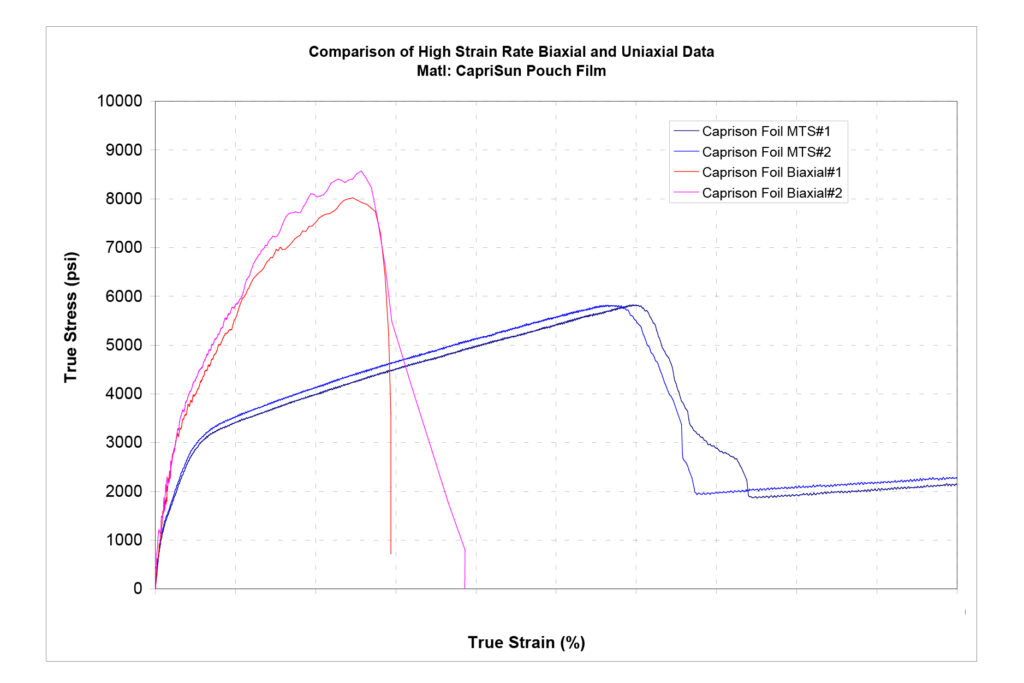
Figure 5. Comparison of bi-axial and uni-axial test data.

Figure 6. Test data for the multi-layer film (Figure 5) is used in the CapriSun package.
Application
One example where biaxial data is uniquely valuable is in the analysis of drop loading for fluid or solids filled flexible pouches, such as the type illustrated in Figure 7.

Figure 7. Flexible packaging for consumer products
Non-linear finite element methods have been used to predict the performance of the package when subject to a drop loading. In order to predict the failure of the package it is necessary to characterize the failure of the material when subjected to high strain rate bi-axial loading. Figure 8 shows a finite element model of a fluid-filled pouch. The computational model of the pouch is dropped onto a rigid surface and the structural response of the package is calculated. The material behavior of the composite film has been established via the bi-axial test and included in the predictive finite element model.

Figure 8. Finite element model of a fluid- filled flexible pouch
Figure 9 shows the progression of the deformation and ultimate failure of the material as a result of the drop. For this type of loading situation, the failure of the composite film is governed by the bi-axial stress state.
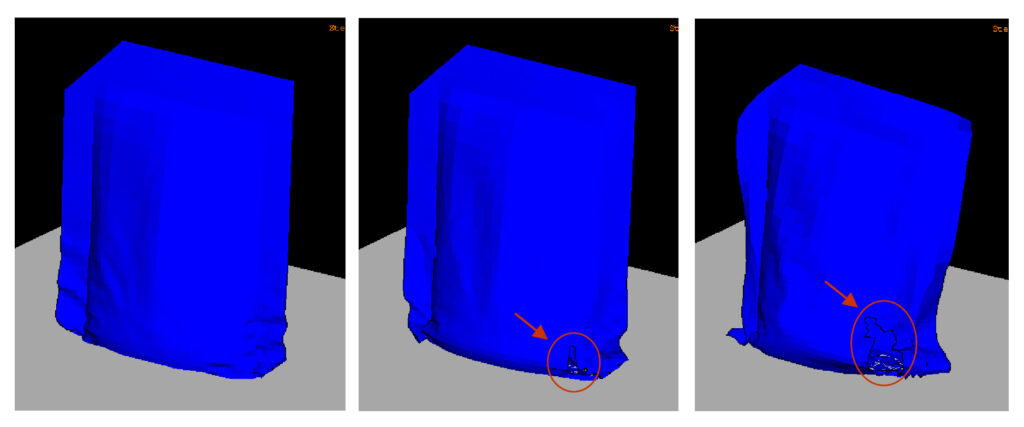
Figure 9. Finite element simulation of flexible package drop, including material failure
Conclusions
Bi-axial stress is frequently the life-limiting stress state for a wide range of products and packages when in use. Uniaxial stress-strain data typically overstate the ductility of a material and is inadequate for judging material performance when the stress state is bi-axial. By using the biaxial inflation test system described herein to obtain bi-axial stress vs. strain data for films and thin rigid plastics, important strain-to-failure information can be used to screen candidate materials and provide input data for predictive structural simulation of packages, products, and processes.
Ref: W004-CPP-Characterizing Flexible Packaging Films & Thin Rigid Plastics
References
[1] Lawrence E. Nielson and Robert F. Landel, Mechanical Properties of Polymers and Composites, Second Edition, Marcel Dekkar, Inc., New York, 1994.
[2] John D. Ferry, Viscoelastic Properties of Polymers, Third Edition, John Wiley and Sons, New York, 1980.
[3] R. M. Christensen and W. W. Feng, Nonlinear Analysis of the Inflation of an Initially Flat, Circular, Elastic Disk, National Laboratory, University of California, Livermore, California 94550.
[4] Axel Products, Inc. Website, axelproducts.com
Ref: W004-CPP-Characterizing Flexible Packaging Films and Thin Rigid Plastics
